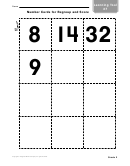
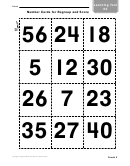
Composite Numbers, Prime Numbers, And 1 Worksheet printable pdf download

Composite Numbers, Prime Numbers, And 1 Worksheet

Composite Numbers, Prime Numbers, and 1

The natural numbers are the numbers 1, 2, 3, 4, 5, . . ., and so on. Among natural numbers, we

distinguish three types of numbers:

1. Composite numbers: These are numbers that can be written as a product of two smaller

numbers. For example, 6 = 2 3.

2. Prime numbers: Everything that isn’t a composite, except 1, is a prime number. Thus a

prime number cannot be written as a product of smaller numbers. For example, 5 is a prime

number.

3. Numbers that are 1: There is only one such number. The number 1 is neither prime nor

composite.

Starting with a composite number, we know (since it’s composite) that we can break it down into

smaller pieces, For example, if we take the number 520, we can break it down into the factors 52

and 10. Each of these decomposes further, for example 52 = 4 13 and 10 = 2 5. We can break

down 6 a little more, into 6 = 2 3, and then rearrange everything that’s left into increasing order:

520 = 52 10 = 4 13 2 5 = 2 2 13 2 5 = 2 2 2 5 13.

It’s clear we can keep going until we can’t go anymore. The numbers we are left with are numbers

that can’t be broken into smaller factors, and we call these prime numbers.

What if we start diﬀerently? We could start with 520 = 8 65, and keep going to get

520 = 8 65 = 2 4 5 13 = 2 2 2 5 13.

Of course, if we start with a prime number instead of a composite number, there’s nothing left to

do.

What is not clear is that given any number, this process of decomposition, no matter how it is

performed, results in a unique answer. This fact deserves a special name:

The Fundamental Theorem of Arithmetic.

Any natural number diﬀerent from

1 can be uniquely represented as a product of primes in increasing order.

Composite Numbers, Prime Numbers, And 1 Worksheet