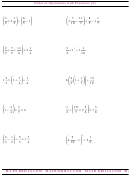Ordered Pairs, Intercepts, And Slopes Worksheet Page 2
ADVERTISEMENT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18Chapter — Graphng
b
m
L
uiLding
AthemAticAL
AnguAge
Linear Equations
Equations in two variables are classified by the exponent (power) of the variables. First degree equations,
that is, equations whose variables are raised to the first power, are
. That means that
linear equations
when these equations are graphed in the Rectangular Coordinate System, their graphs make a straight
line.
Linear equations fit a pattern that looks like Ax + By = C, where x and y are the variables and A, B, and C
are real number constants with A and B not both equal to zero. Ax + By = C is called the
standard form
equation of a line.
y
For example, the equation 2x + 3y = 10 is a linear equation
with infinitely many solutions; (2, 2), (5, 0), and (–1, 4)
are just a few of them. You can see from the graph of this
y-intercept
line (the figure at right) that solutions to a linear equation
(-1, 4)
(2, 2)
are points on the graph of that equation.
x-intercept
x and y-Intercepts
x
(5, 0)
There are two
that convey
ordered pair solutions
extra information and that have special names, the x- and
y-intercepts. The
is the point at which the
x-intercept
graph of the line crosses the x-axis. As you can see in the
figure at right, that point is (5, 0). It is important to note
that the y-coordinate of this point is zero. Similarly, the
is the point at which the graph of the line
y-intercept
crosses the y-axis. The x-coordinate at this point is zero. Though we have not plotted this point on the
graph of the line, you can see that it does exist at the point where the line crosses the y-axis.
The x and y-intercepts allow us to find two ordered pair solutions with minimal effort.
The point at which the line crosses the x-axis is the x-intercept at (x, 0).
The point at which the line crosses the y-axis is the y-intercept at (0, y).
y = mx + b: The Slope-Intercept Form of the Equation of a Line
There is a special form of the equation for a line that allows us to read information directly from it. The
for the equation of a line looks like y = mx + b. From the slope-intercept form
slope-intercept form
of an equation, we can determine two important pieces of information by inspection—just by reading the
equation.
y =
x +
m
b
The first is m, the coefficient of x. That value has special meaning
for the graph of the line. It is the
of the line, or how steep
slope
or inclined the line is. The value b in the slope-intercept form
slope
y-intercept
indicates the second piece of information, the y-intercept, which
is the point (0, b).
ADVERTISEMENT
0 votes
Related Articles
Related forms
Related Categories
Parent category: Education