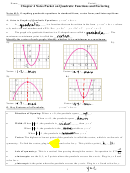
1-5 Parent Functions And Transformations Worksheet With Answers
ADVERTISEMENT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18has an intercept at (0, 0). The graph is symmetric
with respect to the y-axis. The graph is continuous.
and
. The graph is
1-5 Parent Functions and Transformations
decreasing on (− , 0) and increasing on (0,
).
Describe the following characteristics of the
5.
f (x) = c
graph of each parent function: domain, range,
ANSWER:
intercepts, symmetry, continuity, end behavior,
and intervals on which the graph is
D = {x | x
R}, R = {y | y = c, c
R}. If c = 0, all
increasing/decreasing.
real numbers are x-intercepts. If c ≠ 0, there are no
1.
f (x) = §x¨
x-intercepts. The graph has a y-intercept at (0, c). If
c ≠ 0, the graph is symmetric with respect to the y-
ANSWER:
axis. If c = 0, the graph is symmetric with respect to
D = {x | x
R}, R = {y | y
Z}. The graph has a y-
the x-axis, y-axis, and origin. The graph is
intercept at (0, 0) and x-intercepts for {x | 0 ≤ x < 1,
continuous.
and
. The
x
R}. The graph has no symmetry. The graph has
graph is constant on (− , ).
a jump discontinuity for {x | x
Z}.
= −
6.
=
and
. The graph is constant for {x | x
f (x) = x
Z}. The graph increases for {x | x
Z}.
ANSWER:
D = {x | x
R}, R = {y | y R}. The graph has an
intercept at (0, 0). The graph is symmetric with
2.
f (x) =
respect to the origin. The graph is continuous.
and
. The graph is
ANSWER:
increasing on (− , ).
D = {x | x ≠ 0, x
R}, R = {y | y ≠ 0, y
R}. The
graph has no intercepts. The graph is symmetric with
Use the graph of f (x) =
to graph each
respect to the origin. The graph has an infinite
function.
discontinuity at x = 0.
= 0 and
=
7.
g(x) =
0. The graph is decreasing on (− , 0) and (0,
).
ANSWER:
3
3.
f (x) = x
ANSWER:
D = {x | x
R}, R = {y | y
R}. The graph has an
intercept at (0, 0). The graph is symmetric with
respect to the origin. The graph is continuous.
= −
and
=
. The graph is
increasing on (− , ).
4
4.
f (x) = x
8.
g(x) =
ANSWER:
ANSWER:
D = {x | x
R}, R = {y | y ≥ 0, y
R}. The graph
has an intercept at (0, 0). The graph is symmetric
with respect to the y-axis. The graph is continuous.
and
. The graph is
decreasing on (− , 0) and increasing on (0,
).
5.
f (x) = c
ANSWER:
D = {x | x
R}, R = {y | y = c, c
R}. If c = 0, all
9.
g(x) =
– 4
real numbers are x-intercepts. If c ≠ 0, there are no
eSolutions Manual - Powered by Cognero
Page 1
x-intercepts. The graph has a y-intercept at (0, c). If
ANSWER:
c ≠ 0, the graph is symmetric with respect to the y-
axis. If c = 0, the graph is symmetric with respect to
ADVERTISEMENT
0 votes
Related Articles
Related forms
Related Categories
Parent category: Education