Circles Worksheets With Answer Keys - Chapter 7.2 Hooked On Conics, Stitz-Zeager Precalculus Book
ADVERTISEMENT
498
Hooked on Conics
7.2
Circles
Recall from Geometry that a circle can be determined by fixing a point (called the center) and a
positive number (called the radius) as follows.
Definition 7.1. A circle with center (h, k) and radius r > 0 is the set of all points (x, y) in the
plane whose distance to (h, k) is r.
(x, y)
r
(h, k)
From the picture, we see that a point (x, y) is on the circle if and only if its distance to (h, k) is r.
We express this relationship algebraically using the Distance Formula, Equation 1.1, as
r =
(x
+ (y
h)
2
k)
2
By squaring both sides of this equation, we get an equivalent equation (since r > 0) which gives us
the standard equation of a circle.
Equation 7.1. The Standard Equation of a Circle: The equation of a circle with center
(h, k) and radius r > 0 is (x
+ (y
= r
2
2
2
h)
k)
.
Example 7.2.1. Write the standard equation of the circle with center ( 2, 3) and radius 5.
Solution. Here, (h, k) = ( 2, 3) and r = 5, so we get
(x
( 2))
+ (y
3)
= (5)
2
2
2
(x + 2)
+ (y
3)
= 25
2
2
Example 7.2.2. Graph (x + 2)
+ (y
1)
= 4. Find the center and radius.
2
2
Solution. From the standard form of a circle, Equation 7.1, we have that x + 2 is x
h, so h =
2
and y
1 is y
k so k = 1. This tells us that our center is ( 2, 1). Furthermore, r
= 4, so r = 2.
2
Thus we have a circle centered at ( 2, 1) with a radius of 2. Graphing gives us
ADVERTISEMENT
0 votes
Related Articles
Related forms
Related Categories
Parent category: Education
 1
1 2
2 3
3 4
4 5
5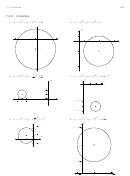 6
6 7
7