Linear Equations In Two Variables Worksheet
ADVERTISEMENT
Linear Equations in Two Variables
In this chapter, we’ll use the geometry of lines to help us solve equations.
Linear equations in two variables
If a, b, and r are real numbers (and if a and b are not both equal to 0) then
ax + by = r is called a linear equation in two variables. (The “two variables”
are the x and the y.)
The numbers a and b are called the coe cients of the equation ax + by = r.
The number r is called the constant of the equation ax + by = r.
Examples. 10x
3y = 5 and
2x
4y = 7 are linear equations in two
variables.
Solutions of equations
A solution of a linear equation in two variables ax+by = r is a specific point
in R
2
such that when when the x-coordinate of the point is multiplied by a,
and the y-coordinate of the point is multiplied by b, and those two numbers
are added together, the answer equals r. (There are always infinitely many
solutions to a linear equation in two variables.)
Example. Let’s look at the equation 2x
3y = 7.
Notice that x = 5 and y = 1 is a point in R
2
that is a solution of this
equation because we can let x = 5 and y = 1 in the equation 2x
3y = 7
and then we’d have 2(5)
3(1) = 10
3 = 7.
The point x = 8 and y = 3 is also a solution of the equation 2x
3y = 7
since 2(8)
3(3) = 16
9 = 7.
The point x = 4 and y = 6 is not a solution of the equation 2x
3y = 7
because 2(4)
3(6) = 8
18 =
10, and
10 = 7.
To get a geometric interpretation for what the set of solutions of 2x 3y = 7
looks like, we can add 3y, subtract 7, and divide by 3 to rewrite 2x
3y = 7
2
7
2
as
x
= y. This is the equation of a line that has slope
and a y-intercept
3
3
3
7
of
. In particular, the set of solutions to 2x
3y = 7 is a straight line.
3
(This is why it’s called a linear equation.)
244
ADVERTISEMENT
0 votes
Related Articles
Related forms
Related Categories
Parent category: Education
 1
1 2
2 3
3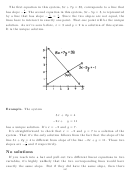 4
4 5
5 6
6 7
7








