Deriving Relationships From Graphs (Page 2 of 2) in pdf

Non-linear Relationships:

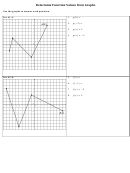
The graph to the left is a hyperbolic relationship. That is, the data

are not linear and both sets of values appear to approach

asymptotes. There are two approaches that one might use to find

the relationship between the variables pressure and volume. One

can perform a non-linear regression analysis to find the

relationship using a calculator or computer, or linearize the plot by

manipulating the data and re-plotting in an effort to create a linear

relationship between the manipulated variables. Looking at the

data carefully suggests that we have here an inverse relationship.

That is, when pressure is doubled, the volume is halved. The

relationship between the variables would seem to be of the form

pressure is inversely proportional to volume. Assuming for a

moment that this is the case, data for either pressure or volume can

be inverted (e.g., replace by 1/var) and the data re-graphed to see if

a linear relationship results. Replacing volume by 1/volume results in the graph below.

Linearized Plot of Above Data:

Here we see a linearized plot of the pressure-volume data used to

create the graph above. On the horizontal axis of the graph the

inverse of the volume has been plotted; pressure is plotted as

before on the vertical axis. A linear fit of the type y = mx + b is

now possible and shows that a linear relationship exists between

pressure and the inverse of the volume in this particular situation.

Note that the x-variable is identified with 1/volume, that the y-

variable is identified with 1/volume, and that b = 0. That is,

pressure = (3atm*lit)/volume

pressure * volume = 3atm*lit

The “Simpler, More Natural” Fit:

Students are sometimes tempted to use a polynomial function to

conduct a non-linear curve fit using calculators or computers (e.g.,

y = a + bx + cx

+ dx

+ ex

+ fx

+…). Such a function will fit

almost any data so long as the degree of the function is high

enough. What sometimes happens though (as did not happen in the

graph to the left) is that there will be wild migrations of the best-fit

curve between the data points that probably wouldn’t happen in

nature. Fortunately, Mother Nature is less complex than that, and

best fits involving trigonometric functions and the like can provide

simpler forms of relationship. Note the 4

order power function fit

of the graph to the left. A trigonometric function given by intensity

= (2.5lux)cos(θ) is a “simpler” representation of the data and a

“more natural” fit with the data. As a rule, simpler interpretations

are valued over more complex in science.

Deriving Relationships From Graphs Page 2

Related Articles

Related forms

Related Categories