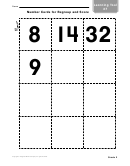
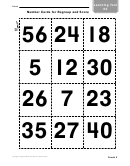
Composite Numbers, Prime Numbers, And 1 Worksheet (Page 3 of 3) in pdf

Composite Numbers, Prime Numbers, And 1 Worksheet Page 3

Primes of the form

We can split the odd primes into two distinct groups: those of the form 4k + 1 (the ﬁrst few being

5, 13, 17, 29, 37, . . .), and those of the form 4k + 3 (the ﬁrst few being 3, 7, 11, 19, 23, . . .). Since we

know there are inﬁnitely many primes (and only one even prime!), at least one of these two groups

must be inﬁnite. Using an argument similar to Euclid’s proof for all primes, we can show that there

are inﬁnitely many primes of the form 4k + 3. (In fact there are also inﬁnitely many of the form

4k + 1, but this is more diﬃcult to show.)

1. Show that if you multiply together any two numbers of the form 4k + 1 (for instance, 4m + 1

and 4n + 1), you get another number of that form.

2. Explain why any number of the form 4k + 3 has a prime factor of the same form.

3. Now we want to show that there are inﬁnitely many primes of the form 4k+3. Like in Euclid’s

proof, we will start by assuming the

: namely, that there are only ﬁnitely many primes

of this form–and from this try to reach some impossible conclusion, a contradiction.

So assume there are only ﬁnitely many primes of the form 4k + 3—call them p

, p

, . . . , p .

Then consider the number N = 4p

p + 3. What can you say about this number? In

particular, which if any of the p ’s is it divisible by?

4. Actually, the number N as deﬁned above

divisible by one of the p ’s. Change the deﬁnition

of N slightly so it’s still of the form 4k + 3, but is no longer divisible by any of the primes p

of this form. Why is this a contradiction?

Composite Numbers, Prime Numbers, And 1 Worksheet Page 3