Chapter 4 Notes Packet On Quadratic Functions And Factoring Worksheet With Answers - Algebra 2
ADVERTISEMENT
Name:_______________________________
Period:____
Chapter 4 Notes Packet on Quadratic Functions and Factoring
Notes #15: Graphing quadratic equations in standard form, vertex form, and intercept form.
=
+
+
2
A. Intro to Graphs of Quadratic Equations:
y
ax
bx c
•
=
+
+ where
2
A ____________________ is a function that can be written in the form
y
ax
bx c
≠
=
= −
+
=
− −
2
2
2
a, b, and c are real numbers and a
0. Ex:
y
5
x
y
2
x
7
y
x
x
3
•
The graph of a quadratic function is a U-shaped curve called a ________________. The
maximum or minimum point is called the _____________
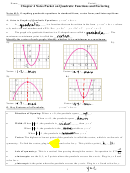
Identify the vertex of each graph; identify whether it is a minimum or a maximum.
1.)
2.)
Vertex: (
,
) _________
Vertex: (
,
) _________
3.)
4.)
Vertex: (
,
) _________
Vertex: (
,
) _________
=
+
+
2
B. Key Features of a Parabola:
y
ax
bx c
•
a > , the parabola opens ________:
Direction of Opening: When
0
a < , the parabola opens ________:
When
0
•
a < , the parabola is _______________ than
=
2
Width: When
1
y
x
a = , the parabola is the ________ width as
=
2
When
y
x
1
a > , the parabola is ________ than
=
2
When
1
y
x
•
Vertex: The highest or lowest point of the parabola is called the vertex, which is on the axis of
−
b
=
x
symmetry. To find the vertex, plug in
and solve for y. This yields a point (____, ____)
2
a
−
b
=
•
x
Axis of symmetry: This is a vertical line passing through the vertex. Its equation is:
2
a
•
x-intercepts: are the 0, 1, or 2 points where the parabola crosses the x-axis. Plug in y = 0 and
solve for x.
•
y-intercept: is the point where the parabola crosses the y-axis. Plug in x = 0 and solve for y.
1
ADVERTISEMENT
1 votes
Related Articles
Related forms
Related Categories
Parent category: Education
 1
1 2
2 3
3 4
4 5
5








