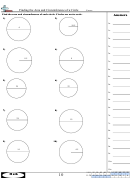
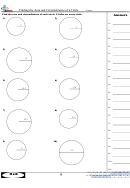
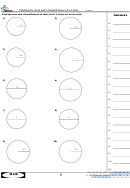
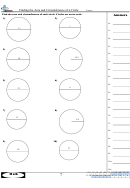
Similar Triangles, Right Triangles, And The Definition Of The Sine, Cosine And Tangent Functions Of Angles Of A Right Triangle Worksheets With Answer Key Page 34
ADVERTISEMENT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43TRIGONOMETRIC EQUATIONS
Most of the trigonometric equations we have seen up to this point have been identities; i.e., they were
true for all values of the variables. Now we wish to consider conditional equations –– ones which are
true for some, but not all, values of the variables. To solve a conditional equation means to find all
values of the variables for which the equality holds.
θ
θ
Example: The trigonometric equation sin
= 1 is true for some values of
and not for others. It
θ
π
θ
is not true for
=
, neither is it true for
= your social security number. There
6
are an infinite number of solutions to this equation. They are given by
π
θ
π
=
±
2
n
,
where n is an integer.
2
Some trigonometric equations don't have any solutions; i.e., they are not true for any of the variables.
θ
θ
Example: Solve sin
= 3 - cos
.
θ
θ
θ
θ
θ
Solution: Rewrite this equation as sin
+ cos
= 3. For every value of
, sin
+ cos
< 2.
θ
θ
θ
Therefore, there are no values of
for which sin
+ cos
= 3. Hence, this equation has
no solutions.
There is no general procedure for solving all trigonometric equations and some can be very difficult.
θ
θ
For example, you might try your hand at the innocent-looking tan
=
. (After you run out of good
ideas with identities and algebraic manipulations, you might get out your calculator and try some
approximations.)
We will be concerned only with equations that can be solved by using trigonometric identities to
change the form of the equation and applying algebraic methods such as rearranging terms, factoring,
squaring, and taking roots.
The simplest trigonometric equations are
θ
θ
θ
sin
= c, cos
= c and tan
= c,
where c is a constant. Inverse trigonometric functions can be used to find one solution to equations of
this form, when the equation has a solution. Our problem is to use this information to find all
solutions.
θ
θ
θ
π
= c have two solutions in the interval 0 ≤
The equations sin
= c and cos
< 2
when |c| < 1, and one
π
solution when |c| = 1. Since the sine and cosine functions have period 2
, to find all solutions, add and
π
θ
π
to the solutions in the interval 0 ≤
subtract integer multiples of 2
< 2
.
θ
θ
π
= c has one solution in the interval 0 ≤
For any number c, the equation tan
<
. Since the tangent
π
π
function has period
, to find all solutions, add integer multiples of
to the solution in the interval
θ
π
0 ≤
<
.
An expression (or expressions) which describes all solutions to a trigonometric equation in a simple
way is called the general solution to the equation.
1
θ
cos =
Example: Solve the trigonometric equation
.
2
Solution: One solution is
π
1
θ
=
=
1 -
cos
.
1
2
3
θ
π
The second solution in the interval 0 ≤
< 2
is
- 34 -
ADVERTISEMENT
0 votes
Related Articles
Related forms
Related Categories
Parent category: Education